The discrimination of the methylation signal from the stochastic methylation
background resultant from the standard (non-stressful) biological processes is
a critical step for the genome-wide methylation analysis. Such a
discrimination requires for the knowledge of the probability distribution of
the information divergence of methylation levels and a proper evaluation of
the classification performance of differentially methylated positions (DMPs)
into two classes: DMPs from control and DMPs from treatment.
Background
The probability of extreme methylation changes occurring spontaneously in a
control population by the stochastic fluctuations inherent to biochemical
processes and DNA maintenance (1), requires the discrimination of this
background variation from a biological treatment signal. The stochasticity of
the the methylation process derives from the stochasticity inherent to
biochemical processes (2–3). There are fundamental physical
reasons to acknowledge that biochemical processes are subject to noise and
fluctuations (4–5). So, regardless constant environment,
statistically significant methylation changes can be found in control population with probability greater than zero and proportional to a Boltzmann factor (6).
Natural signals and those generated by human technology are not free of noise
and, as mentioned above, the methylation signal is no exception. Only signal
detection based approaches are designed to filter out the signal from the noise,
in natural and in human generated signals.
The stochasticity of methylation regulatory machinery effects is presumed to
reflect system heterogeneity; cells from the same tissue are not necessarily in
the same state, and therefore, corresponding cytosine sites differ in their
methylation status. Consequently, overall organismal response is conveyed as a
statistical outcome that distinguishes the regulatory methylation signal from
statistical background “noise”. Estimation of optimal cutoff value for the
signal is an additional step to remove any remaining potential methylation
background noise with probability $0 ≤ \alpha ≤ 0.05$. We define as a
methylation signal (DMP) each cytosine site with Hellinger Divergence values above the cutpoint (shown in (7)).
As a result, a differentially methylated position (DMP) as a cytosine position
with high probability to be altered in methylation due to a treatment effect,
distinct from spontaneous variation detected in the control population.
Note: This example was made with the MethylIT version 0.3.2 available at https://github.com/genomaths/MethylIT.
Data generation
For the current example on methylation analysis with Methyl-IT we will use
simulated data. Read-count matrices of methylated and unmethylated cytosine are
generated with MethylIT.utils function simulateCounts. A standard analysis of this
dataset is given in the web page: Methylation analysis with Methyl-IT
library(MethylIT)
library(MethylIT.utils)
bmean <- function(alpha, beta) alpha/(alpha + beta)
alpha.ct <- 0.09
alpha.tt <- 0.2
# The number of cytosine sites to generate
sites = 50000
# Set a seed for pseudo-random number generation
set.seed(124)
control.nam <- c("C1", "C2", "C3")
treatment.nam <- c("T1", "T2", "T3")
# Reference group
ref0 = simulateCounts(num.samples = 4, sites = sites, alpha = alpha.ct, beta = 0.5,
size = 50, theta = 4.5, sample.ids = c("R1", "R2", "R3", "R4"))
# Control group
ctrl = simulateCounts(num.samples = 3, sites = sites, alpha = alpha.ct, beta = 0.5,
size = 50, theta = 4.5, sample.ids = control.nam)
# Treatment group
treat = simulateCounts(num.samples = 3, sites = sites, alpha = alpha.tt, beta = 0.5,
size = 50, theta = 4.5, sample.ids = treatment.nam)
# Reference sample
ref = poolFromGRlist(ref0, stat = "mean", num.cores = 4L, verbose = FALSE)
Methylation level divergences
Total variation distance and Hellinger divergence are computed with estimateDivergence
function
divs <- estimateDivergence(ref = ref, indiv = c(ctrl, treat), Bayesian = TRUE,
num.cores = 6L, percentile = 1, verbose = FALSE)
To get some statistical description about the sample is useful. Here, empirical
critical values for the probability distribution of $H$ and $TV$ can is obtained
using quantile function from the R package stats.
critical.val <- do.call(rbind, lapply(divs, function(x) {
x <- x[x$hdiv > 0]
hd.95 = quantile(x$hdiv, 0.95)
tv.95 = quantile(abs(x$TV), 0.95)
return(c(tv = tv.95, hd = hd.95))
}))
critical.val
## tv.95
## C1 0.6842105 66.76081
## C2 0.6800000 66.71995
## C3 0.6777456 65.98495
## T1 0.9397681 138.68237
## T2 0.9478351 141.72637
## T3 0.9466565 141.77241
Estimation of potential DMPs with Methyl-IT
In Methyl-IT, DMP estimation requires for the knowledge of the probability distribution
of the noise (plus signal), which is used as null hypothesis.
The best fitted distribution model can be estimated with function
gofReport.
Here, for illustration purposes, we will use specific estimations based on 2-
and 3-parameter gamma distribution models directly using function nonlinearFitDist.
Potential DMPs estimated with 2-parameter gamma distribution model
nlms.g2p <- nonlinearFitDist(divs, column = 9L, verbose = FALSE, num.cores = 6L,
dist.name = "Gamma2P")
# Potential DMPs from 'Gamma2P' model
pDMPs.g2p <- getPotentialDIMP(LR = divs, nlms = nlms.g2p, div.col = 9L,
tv.cut = 0.68, tv.col = 7, alpha = 0.05,
dist.name = "Gamma2P")
Potential DMPs estimated with 3-parameter gamma distribution model
nlms.g3p <- nonlinearFitDist(divs, column = 9L, verbose = FALSE, num.cores = 6L,
dist.name = "Gamma3P")
# Potential DMPs from 'Gamma2P' model
pDMPs.g3p <- getPotentialDIMP(LR = divs, nlms = nlms.g3p, div.col = 9L,
tv.cut = 0.68, tv.col = 7, alpha = 0.05,
dist.name = "Gamma3P")
Cutpoint estimation
As a result of the natural spontaneous variation, naturally occurring DMPs can
be identified in samples from the control and treatment populations.
Machine-learning algorithms implemented in Methyl-IT are applied to discriminate
treatment-induced DMPs from those naturally generated.
The simple cutpoint estimation available in Methyl-IT is based on the
application of Youden index (8). Although cutpoints are estimated for
a single variable, the classification performance can be evaluated for several
variables and applying different model classifiers.
In the current example, the column carrying TV (div.col = 7L) will be used
to estimate the cutpoint. The column values will be expressed in terms of
$TV_d=|p_{tt}-p_{ct}|$. A minimum cutpoint value for TV derived from the
minimum 95
applied (see Methylation analysis with
Methyl-IT).
Next, a logistic model classifier will be fitted with the 60
of the raw data (training set) and then the resting 40
will be used to evaluate the model performance. The predictor variable included
in the model are specified with function parameter column (for more detail see estimateCutPoint
or type ?estimateCutPoint in R console).
Simple cutpoint estimation for Gamma2P model
Here, we use the results of modeling the distribution of the Hellinger
divergence (HD) of methylation levels through a 2-parameter gamma probability
distribution model. The critical values for $HD_{\alpha = 0.05}^{CT_{G2P}}$ used
to get potential DMPs were:
nams <- names(nlms.g2p)
crit <- unlist(lapply(nlms.g2p, function(x) qgamma(0.95, shape = x$Estimate[1],
scale = x$Estimate[2])))
names(crit) <- nams
crit
## C1 C2 C3 T1 T2 T3
## 58.59180 57.99972 57.81016 112.40001 113.92362 114.48802
As before the cutpoint is estimated based on ‘Youden Index’ (8). A
PCA+LDA model classifier (classifier = "pca.lda") is applied. That is, a
principal component analysis (PCA) is applied on the original raw matrix of data
and the four possible component (n.pc = 4) derived from the analysis are used
in a further linear discriminant analysis (LDA). A scaling step is applied to
the raw matrix of data before the application of the mentioned procedure
(center = TRUE, scale = TRUE). Here, PCA will yield new orthogonal
(non-correlated) variables, the principal components, which prevent any
potential bias effect originated by any correlation or association of the
original variables.
By using function
estimateCutPoint,
we can estimate the cutpoint, based on HD (div.col = 9L) or on $TV_d$
(div.col = 7L):
# Cutpoint estimation for the FT approach using the ECDF critical value
cut.g2p = estimateCutPoint(LR = pDMPs.g2p, simple = TRUE,
column = c(hdiv = TRUE, bay.TV = TRUE,
wprob = TRUE, pos = TRUE),
classifier1 = "pca.lda", n.pc = 4,
control.names = control.nam,
treatment.names = treatment.nam,
center = TRUE, scale = TRUE,
clas.perf = TRUE, prop = 0.6,
div.col = 9L)
cut.g2p
## Cutpoint estimation with 'Youden Index'
## Simple cutpoint estimation
## Cutpoint = 114.22
##
## Cytosine sites from treatment have divergence values >= 114.22
##
## The accessible objects in the output list are:
## Length Class Mode
## cutpoint 1 -none- numeric
## testSetPerformance 6 confusionMatrix list
## testSetModel.FDR 1 -none- numeric
## model 2 pcaLDA list
## modelConfMatrix 6 confusionMatrix list
## initModel 1 -none- character
## postProbCut 1 -none- logical
## postCut 1 -none- logical
## classifier 1 -none- character
## statistic 1 -none- logical
## optStatVal 1 -none- logical
## cutpData 1 -none- logical
## initModelConfMatrix 6 confusionMatrix list
As indicated above, the model classifier performance and its corresponding false
discovery rate can be retrieved as:
cut.g2p$testSetPerformance
## Confusion Matrix and Statistics
##
## Reference
## Prediction CT TT
## CT 319 0
## TT 0 3544
##
## Accuracy : 1
## 95
## No Information Rate : 0.9174
## P-Value [Acc > NIR] : < 2.2e-16
##
## Kappa : 1
##
## Mcnemar's Test P-Value : NA
##
## Sensitivity : 1.0000
## Specificity : 1.0000
## Pos Pred Value : 1.0000
## Neg Pred Value : 1.0000
## Prevalence : 0.9174
## Detection Rate : 0.9174
## Detection Prevalence : 0.9174
## Balanced Accuracy : 1.0000
##
## 'Positive' Class : TT
##
cut.g2p$testSetModel.FDR
## [1] 0
Here, DMP classification is modeled with PCA+QDA classifier (classifier =
"pca.lda"). That is, principal component analysis (PCA) is applied on the
original raw matrix of data and the four possible component (n.pc = 4) are
used in a further linear discriminant analysis (LDA). A scaling step is applied
to the raw matrix of data before the application of the mentioned procedure
(center = TRUE, scale = TRUE).
Next, a different model classifier can be applied to model the classification
derived from the previous cutpoint estimation.
Simple cutpoint estimation for Gamma3P model
The same analyses for the cutpoint estimation can be performed for 3P gamma model
# Cutpoint estimation for the FT approach using the ECDF critical value
cut.g3p = estimateCutPoint(LR = pDMPs.g3p, simple = TRUE,
column = c(hdiv = TRUE, bay.TV = TRUE,
wprob = TRUE, pos = TRUE),
classifier1 = "pca.lda", n.pc = 4,
control.names = control.nam,
treatment.names = treatment.nam,
center = TRUE, scale = TRUE,
clas.perf = TRUE, prop = 0.6,
div.col = 9L)
cut.g3p
## Cutpoint estimation with 'Youden Index'
## Simple cutpoint estimation
## Cutpoint = 115.24
##
## Cytosine sites from treatment have divergence values >= 115.24
##
## The accessible objects in the output list are:
## Length Class Mode
## cutpoint 1 -none- numeric
## testSetPerformance 6 confusionMatrix list
## testSetModel.FDR 1 -none- numeric
## model 2 pcaLDA list
## modelConfMatrix 6 confusionMatrix list
## initModel 1 -none- character
## postProbCut 1 -none- logical
## postCut 1 -none- logical
## classifier 1 -none- character
## statistic 1 -none- logical
## optStatVal 1 -none- logical
## cutpData 1 -none- logical
## initModelConfMatrix 6 confusionMatrix list
As indicated above, the model classifier performance and its corresponding false
discovery rate can be retrieved as:
cut.g3p$testSetPerformance
## Confusion Matrix and Statistics
##
## Reference
## Prediction CT TT
## CT 309 0
## TT 0 3483
##
## Accuracy : 1
## 95
## No Information Rate : 0.9185
## P-Value [Acc > NIR] : < 2.2e-16
##
## Kappa : 1
##
## Mcnemar's Test P-Value : NA
##
## Sensitivity : 1.0000
## Specificity : 1.0000
## Pos Pred Value : 1.0000
## Neg Pred Value : 1.0000
## Prevalence : 0.9185
## Detection Rate : 0.9185
## Detection Prevalence : 0.9185
## Balanced Accuracy : 1.0000
##
## 'Positive' Class : TT
##
cut.g3p$testSetModel.FDR
## [1] 0
DMP prediction based on classification models
The model obtained in the previous step can be used for further prediction with
function
predict
from MethylIT.utils package. For example, we would take a random sample and run:
set.seed(1)
randsampl <- unlist(pDMPs.g3p)
randsampl <- randsampl[sample.int(length(randsampl), 10)]
pred <- predict(cut.g3p$model, newdata = randsampl)
pred
## $class
## [1] CT TT TT TT TT TT TT TT TT TT
## Levels: CT TT
##
## $posterior
## CT TT
## [1,] 1.000000e+00 1.19242e-08
## [2,] 5.231187e-46 1.00000e+00
## [3,] 2.136182e-45 1.00000e+00
## [4,] 6.739051e-47 1.00000e+00
## [5,] 2.015394e-46 1.00000e+00
## [6,] 2.379968e-46 1.00000e+00
## [7,] 3.473689e-46 1.00000e+00
## [8,] 1.760048e-46 1.00000e+00
## [9,] 7.640639e-47 1.00000e+00
## [10,] 3.254017e-47 1.00000e+00
##
## $x
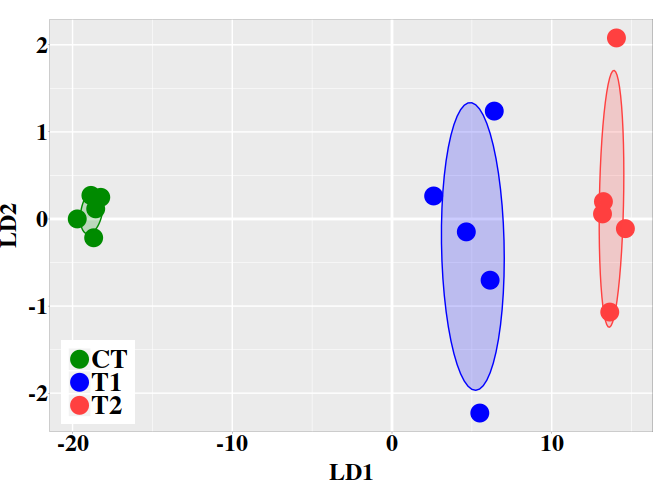
## LD1
## [1,] -7.465499
## [2,] 1.041471
## [3,] 0.943772
## [4,] 1.183774
## [5,] 1.107704
## [6,] 1.096158
## [7,] 1.069901
## [8,] 1.117111
## [9,] 1.175055
## [10,] 1.234328
The variable pred$posterior provides the posterior classification
probabilities that a DMP could belong to control (CT) or to treatment (TT)
group. The variable ‘x‘ provides the cytosine methylation changes in terms of
its values in the linear discriminant function LD1. Notice that, for each row,
the sum of posterior probabilities is equal 1. By default, individuals with TT
posterior probabilities greater than 0.5 are predicted to belong to the
treatment class. For example:
classfiction = rep("CT", 10)
classfiction[pred$posterior[, 2] > 0.5] <- "TT"
classfiction
## [1] "CT" "TT" "TT" "TT" "TT" "TT" "TT" "TT" "TT" "TT"
We can be more strict increasing the posterior classification probability cutoff
classfiction = rep("CT", 10)
classfiction[pred$posterior[, 2] > 0.7] <- "TT"
classfiction
## [1] "CT" "TT" "TT" "TT" "TT" "TT" "TT" "TT" "TT" "TT"
The posterior classification probability cutoff can be controlled with parameter
post.cut from
estimateCutPoint
function (default: $post.cut=0.5$).
Machine-learning (ML) based approach to search for an optimal cutpoint
In the next example the cutpoint estimation for the Hellinger divergence of
methylation levels (div.col = 9L) is accomplished. Function estimateCutPoint
can be used to search for a cutpoint as well. Two model classifiers can be used.
classifiers1 will be used to estimate the posterior classification
probabilities of DMP into those from control and those from treatment. These
probabilities are then used to estimate the cutpoint in the range of values
from, say, 0.5 to 0.8. Next, a classifier2 will be used to evaluate the
classification performance. In this case, the search for an optimal cutpoint is
accomplished maximizing the accuracy (stat = 0) of classifier2.
ML cutpoint estimation for potential DMPs based on Gamma2P model
The ML search for an optimal cutpoint is accomplished in the set of potential
DMPs, which were identified using a Gamma2P probability distribution model as
null hypothesis.
cut.g2p = estimateCutPoint(LR = pDMPs.g2p, simple = FALSE,
column = c(hdiv = TRUE, bay.TV = TRUE,
wprob = TRUE, pos = TRUE),
classifier1 = "pca.lda",
classifier2 = "pca.qda", stat = 0,
control.names = control.nam,
treatment.names = treatment.nam,
cut.values = seq(45, 114, 1), post.cut = 0.5,
clas.perf = TRUE, prop = 0.6,
center = TRUE, scale = TRUE,
n.pc = 4, div.col = 9L)
cut.g2p
## Cutpoint estimation with 'pca.lda' classifier
## Cutpoint search performed using model posterior probabilities
##
## Posterior probability used to get the cutpoint = 0.5
## Cytosine sites with treatment PostProbCut >= 0.5 have a
## divergence value >= 112.4247
##
## Optimized statistic: Accuracy = 1
## Cutpoint = 112.42
##
## Model classifier 'pca.qda'
##
## The accessible objects in the output list are:
## Length Class Mode
## cutpoint 1 -none- numeric
## testSetPerformance 6 confusionMatrix list
## testSetModel.FDR 1 -none- numeric
## model 2 pcaQDA list
## modelConfMatrix 6 confusionMatrix list
## initModel 1 -none- character
## postProbCut 1 -none- numeric
## postCut 1 -none- numeric
## classifier 1 -none- character
## statistic 1 -none- character
## optStatVal 1 -none- numeric
## cutpData 1 -none- logical
Model performance in the test dataset is:
cut.g2p$testSetPerformance
## Confusion Matrix and Statistics
##
## Reference
## Prediction CT TT
## CT 1274 0
## TT 0 3580
##
## Accuracy : 1
## 95
## No Information Rate : 0.7375
## P-Value [Acc > NIR] : < 2.2e-16
##
## Kappa : 1
##
## Mcnemar's Test P-Value : NA
##
## Sensitivity : 1.0000
## Specificity : 1.0000
## Pos Pred Value : 1.0000
## Neg Pred Value : 1.0000
## Prevalence : 0.7375
## Detection Rate : 0.7375
## Detection Prevalence : 0.7375
## Balanced Accuracy : 1.0000
##
## 'Positive' Class : TT
##
Model performance in in the whole dataset is:
cut.g2p$modelConfMatrix
## Confusion Matrix and Statistics
##
## Reference
## Prediction CT TT
## CT 3184 0
## TT 0 8948
##
## Accuracy : 1
## 95
## No Information Rate : 0.7376
## P-Value [Acc > NIR] : < 2.2e-16
##
## Kappa : 1
##
## Mcnemar's Test P-Value : NA
##
## Sensitivity : 1.0000
## Specificity : 1.0000
## Pos Pred Value : 1.0000
## Neg Pred Value : 1.0000
## Prevalence : 0.7376
## Detection Rate : 0.7376
## Detection Prevalence : 0.7376
## Balanced Accuracy : 1.0000
##
## 'Positive' Class : TT
##
The False discovery rate is:
cut.g2p$testSetModel.FDR
## [1] 0
The model classifier PCA+LDA has enough discriminatory power to discriminate
control DMP from those induced by the treatment for HD values
$112.4247 \le HD$.
The probabilities $P(HD \le 122.43)$ to observe a cytosine site with $HD \le
112.4247$ on each individual is:
nams <- names(nlms.g2p)
crit <- unlist(lapply(nlms.g2p, function(x) pgamma(cut.g2p$cutpoint, shape = x$Estimate[1],
scale = x$Estimate[2])))
names(crit) <- nams
crit
## C1 C2 C3 T1 T2 T3
## 0.9964704 0.9966560 0.9967314 0.9500279 0.9483024 0.9476610
In other words, most of the methylation changes are not (and should not be)
considered DMPs. Notice that although the same HD value could be found in the
same differentially methylated cytosine site in control and treatment, if the
probabilities distributions of the information divergences (null hypotheses)
from control and treatment are different, then these DMPs can be distinguished.
ML cutpoint estimation for potential DMPs based on Gamma3P model
Likewise, for the 3-parameter gamma model we can search for an optimal cutpoint:
cut.g3p = estimateCutPoint(LR = pDMPs.g3p, simple = FALSE,
column = c(hdiv = TRUE, TV = TRUE,
wprob = TRUE, pos = TRUE),
classifier1 = "pca.lda",
classifier2 = "pca.qda", stat = 0,
control.names = control.nam,
treatment.names = treatment.nam,
cut.values = seq(45, 114, 1), post.cut = 0.5,
clas.perf = TRUE, prop = 0.6,
center = TRUE, scale = TRUE,
n.pc = 4, div.col = 9L)
cut.g3p
## Cutpoint estimation with 'pca.lda' classifier
## Cutpoint search performed using model posterior probabilities
##
## Posterior probability used to get the cutpoint = 0.5
## Cytosine sites with treatment PostProbCut >= 0.5 have a
## divergence value >= 113.497
##
## Optimized statistic: Accuracy = 1
## Cutpoint = 113.5
##
## Model classifier 'pca.qda'
##
## The accessible objects in the output list are:
## Length Class Mode
## cutpoint 1 -none- numeric
## testSetPerformance 6 confusionMatrix list
## testSetModel.FDR 1 -none- numeric
## model 2 pcaQDA list
## modelConfMatrix 6 confusionMatrix list
## initModel 1 -none- character
## postProbCut 1 -none- numeric
## postCut 1 -none- numeric
## classifier 1 -none- character
## statistic 1 -none- character
## optStatVal 1 -none- numeric
## cutpData 1 -none- logical
DMPs are identified with function selectDIMP
g2p.dmps <- selectDIMP(pDMPs.g2p, div.col = 9L, cutpoint = cut.g2p$cutpoint)
g3p.dmps <- selectDIMP(pDMPs.g3p, div.col = 9L, cutpoint = cut.g3p$cutpoint)
DMPs estimated with Fisher’s exact Test (FT)
For comparison purposes DMPs are estimated with Fisher’s exact test as well.
ft. = FisherTest(LR = divs, tv.cut = 0.68, pAdjustMethod = "BH",
pvalCutOff = 0.05, num.cores = 4L,
verbose = FALSE, saveAll = FALSE)
ft.dmps <- getPotentialDIMP(LR = ft., div.col = 9L, dist.name = "None",
tv.cut = 0.68, tv.col = 7, alpha = 0.05)
Classification performance of DMP classification
After the cutpoint application to select DMPs, a Monte Carlo (bootstrap) analysis
reporting several classifier performance indicators can be accomplished by
using function
evaluateDIMPclass
and its settings output = "mc.val" and num.boot.
Classification performance for DMPs based on Gamma2P model
g2p.class = evaluateDIMPclass(LR = g2p.dmps, control.names = control.nam,
treatment.names = treatment.nam,
column = c(hdiv = TRUE, TV = TRUE,
wprob = TRUE, pos = TRUE),
classifier = "pca.qda", n.pc = 4,
center = TRUE, scale = TRUE, num.boot = 300,
output = "all", prop = 0.6
)
g2p.class$mc.val
## Accuracy Kappa AccuracyLower AccuracyUpper AccuracyNull
## Min. :1 Min. :1 Min. :0.9991 Min. :1 Min. :0.9139
## 1st Qu.:1 1st Qu.:1 1st Qu.:0.9991 1st Qu.:1 1st Qu.:0.9139
## Median :1 Median :1 Median :0.9991 Median :1 Median :0.9139
## Mean :1 Mean :1 Mean :0.9991 Mean :1 Mean :0.9139
## 3rd Qu.:1 3rd Qu.:1 3rd Qu.:0.9991 3rd Qu.:1 3rd Qu.:0.9139
## Max. :1 Max. :1 Max. :0.9991 Max. :1 Max. :0.9139
##
## AccuracyPValue McnemarPValue Sensitivity Specificity Pos Pred Value
## Min. :9.096e-154 Min. : NA Min. :1 Min. :1 Min. :1
## 1st Qu.:9.096e-154 1st Qu.: NA 1st Qu.:1 1st Qu.:1 1st Qu.:1
## Median :9.096e-154 Median : NA Median :1 Median :1 Median :1
## Mean :9.096e-154 Mean :NaN Mean :1 Mean :1 Mean :1
## 3rd Qu.:9.096e-154 3rd Qu.: NA 3rd Qu.:1 3rd Qu.:1 3rd Qu.:1
## Max. :9.096e-154 Max. : NA Max. :1 Max. :1 Max. :1
## NA's :300
## Neg Pred Value Precision Recall F1 Prevalence
## Min. :1 Min. :1 Min. :1 Min. :1 Min. :0.9139
## 1st Qu.:1 1st Qu.:1 1st Qu.:1 1st Qu.:1 1st Qu.:0.9139
## Median :1 Median :1 Median :1 Median :1 Median :0.9139
## Mean :1 Mean :1 Mean :1 Mean :1 Mean :0.9139
## 3rd Qu.:1 3rd Qu.:1 3rd Qu.:1 3rd Qu.:1 3rd Qu.:0.9139
## Max. :1 Max. :1 Max. :1 Max. :1 Max. :0.9139
##
## Detection Rate Detection Prevalence Balanced Accuracy
## Min. :0.9139 Min. :0.9139 Min. :1
## 1st Qu.:0.9139 1st Qu.:0.9139 1st Qu.:1
## Median :0.9139 Median :0.9139 Median :1
## Mean :0.9139 Mean :0.9139 Mean :1
## 3rd Qu.:0.9139 3rd Qu.:0.9139 3rd Qu.:1
## Max. :0.9139 Max. :0.9139 Max. :1
##
Classification performance for DMPs based on Gamma3P model
Likewise the evaluation of the DMP classification performance can be accomplished
for DMPs estimated based on the $’Gamma3P’$ model:
g3p.class = evaluateDIMPclass(LR = g3p.dmps, control.names = control.nam,
treatment.names = treatment.nam,
column = c(hdiv = TRUE, TV = TRUE,
wprob = TRUE, pos = TRUE),
classifier = "pca.qda", n.pc = 4,
center = TRUE, scale = TRUE, num.boot = 300,
output = "all", prop = 0.6
)
g3p.class$mc.val
## Accuracy Kappa AccuracyLower AccuracyUpper AccuracyNull
## Min. :1 Min. :1 Min. :0.999 Min. :1 Min. :0.914
## 1st Qu.:1 1st Qu.:1 1st Qu.:0.999 1st Qu.:1 1st Qu.:0.914
## Median :1 Median :1 Median :0.999 Median :1 Median :0.914
## Mean :1 Mean :1 Mean :0.999 Mean :1 Mean :0.914
## 3rd Qu.:1 3rd Qu.:1 3rd Qu.:0.999 3rd Qu.:1 3rd Qu.:0.914
## Max. :1 Max. :1 Max. :0.999 Max. :1 Max. :0.914
##
## AccuracyPValue McnemarPValue Sensitivity Specificity Pos Pred Value
## Min. :1.393e-150 Min. : NA Min. :1 Min. :1 Min. :1
## 1st Qu.:1.393e-150 1st Qu.: NA 1st Qu.:1 1st Qu.:1 1st Qu.:1
## Median :1.393e-150 Median : NA Median :1 Median :1 Median :1
## Mean :1.393e-150 Mean :NaN Mean :1 Mean :1 Mean :1
## 3rd Qu.:1.393e-150 3rd Qu.: NA 3rd Qu.:1 3rd Qu.:1 3rd Qu.:1
## Max. :1.393e-150 Max. : NA Max. :1 Max. :1 Max. :1
## NA's :300
## Neg Pred Value Precision Recall F1 Prevalence
## Min. :1 Min. :1 Min. :1 Min. :1 Min. :0.914
## 1st Qu.:1 1st Qu.:1 1st Qu.:1 1st Qu.:1 1st Qu.:0.914
## Median :1 Median :1 Median :1 Median :1 Median :0.914
## Mean :1 Mean :1 Mean :1 Mean :1 Mean :0.914
## 3rd Qu.:1 3rd Qu.:1 3rd Qu.:1 3rd Qu.:1 3rd Qu.:0.914
## Max. :1 Max. :1 Max. :1 Max. :1 Max. :0.914
##
## Detection Rate Detection Prevalence Balanced Accuracy
## Min. :0.914 Min. :0.914 Min. :1
## 1st Qu.:0.914 1st Qu.:0.914 1st Qu.:1
## Median :0.914 Median :0.914 Median :1
## Mean :0.914 Mean :0.914 Mean :1
## 3rd Qu.:0.914 3rd Qu.:0.914 3rd Qu.:1
## Max. :0.914 Max. :0.914 Max. :1
##
We do not have evidence to support statistical differences between the
classification performances estimated for ‘Gamma2P’ and ‘Gamma3P’ probability
distribution models. Hence, in this case we select the model that yield the
lowest cutpoint
Classification performance for DMPs based on Fisher’s exact test
Classification performance results obtained with Monte Carlos sampling for the
$Gamma2P$ and $Gamma3P$ models are quite different from those obtained with FT:
ft.class = evaluateDIMPclass(LR = ft.dmps, control.names = control.nam,
treatment.names = treatment.nam,
column = c(hdiv = TRUE, TV = TRUE,
wprob = TRUE, pos = TRUE),
classifier = "pca.lda", n.pc = 4,
center = TRUE, scale = TRUE, num.boot = 300,
output = "all", prop = 0.6
)
ft.class$mc.val
## Accuracy Kappa AccuracyLower AccuracyUpper
## Min. :0.8076 Min. :-0.007635 Min. :0.8001 Min. :0.8148
## 1st Qu.:0.8105 1st Qu.: 0.005355 1st Qu.:0.8031 1st Qu.:0.8177
## Median :0.8110 Median : 0.007678 Median :0.8036 Median :0.8182
## Mean :0.8110 Mean : 0.007553 Mean :0.8036 Mean :0.8182
## 3rd Qu.:0.8115 3rd Qu.: 0.009748 3rd Qu.:0.8041 3rd Qu.:0.8187
## Max. :0.8137 Max. : 0.020669 Max. :0.8064 Max. :0.8209
## AccuracyNull AccuracyPValue McnemarPValue Sensitivity
## Min. :0.8188 Min. :0.9205 Min. :0 Min. :0.9835
## 1st Qu.:0.8188 1st Qu.:0.9781 1st Qu.:0 1st Qu.:0.9857
## Median :0.8188 Median :0.9847 Median :0 Median :0.9863
## Mean :0.8188 Mean :0.9827 Mean :0 Mean :0.9863
## 3rd Qu.:0.8188 3rd Qu.:0.9888 3rd Qu.:0 3rd Qu.:0.9868
## Max. :0.8188 Max. :0.9990 Max. :0 Max. :0.9893
## Specificity Pos Pred Value Neg Pred Value Precision
## Min. :0.01134 Min. :0.8181 Min. :0.1337 Min. :0.8181
## 1st Qu.:0.01726 1st Qu.:0.8193 1st Qu.:0.2150 1st Qu.:0.8193
## Median :0.01874 Median :0.8196 Median :0.2318 Median :0.8196
## Mean :0.01858 Mean :0.8196 Mean :0.2304 Mean :0.8196
## 3rd Qu.:0.02022 3rd Qu.:0.8198 3rd Qu.:0.2455 3rd Qu.:0.8198
## Max. :0.02663 Max. :0.8208 Max. :0.3187 Max. :0.8208
## Recall F1 Prevalence Detection Rate
## Min. :0.9835 Min. :0.8933 Min. :0.8188 Min. :0.8053
## 1st Qu.:0.9857 1st Qu.:0.8950 1st Qu.:0.8188 1st Qu.:0.8071
## Median :0.9863 Median :0.8952 Median :0.8188 Median :0.8076
## Mean :0.9863 Mean :0.8952 Mean :0.8188 Mean :0.8076
## 3rd Qu.:0.9868 3rd Qu.:0.8955 3rd Qu.:0.8188 3rd Qu.:0.8080
## Max. :0.9893 Max. :0.8969 Max. :0.8188 Max. :0.8101
## Detection Prevalence Balanced Accuracy
## Min. :0.9825 Min. :0.4975
## 1st Qu.:0.9848 1st Qu.:0.5017
## Median :0.9853 Median :0.5025
## Mean :0.9854 Mean :0.5024
## 3rd Qu.:0.9860 3rd Qu.:0.5031
## Max. :0.9879 Max. :0.5066
A quite different story is found when information on the probability
distribution of noise (null hypothesis) is added to the classifier:
ft.g2p.dmps <- getPotentialDIMP(LR = ft., nlms = nlms.g2p, div.col = 9L,
tv.cut = 0.68, tv.col = 7, alpha = 0.05,
dist.name = "Gamma2P")
ft.g2p.class = evaluateDIMPclass(LR = ft.g2p.dmps, control.names = control.nam,
treatment.names = treatment.nam,
column = c(hdiv = TRUE, TV = TRUE,
wprob = TRUE, pos = TRUE),
classifier = "pca.lda", n.pc = 4,
center = TRUE, scale = TRUE, num.boot = 300,
output = "all", prop = 0.6
)
ft.g2p.class$mc.val
## Accuracy Kappa AccuracyLower AccuracyUpper AccuracyNull
## Min. :1 Min. :1 Min. :0.9992 Min. :1 Min. :0.7375
## 1st Qu.:1 1st Qu.:1 1st Qu.:0.9992 1st Qu.:1 1st Qu.:0.7375
## Median :1 Median :1 Median :0.9992 Median :1 Median :0.7375
## Mean :1 Mean :1 Mean :0.9992 Mean :1 Mean :0.7375
## 3rd Qu.:1 3rd Qu.:1 3rd Qu.:0.9992 3rd Qu.:1 3rd Qu.:0.7375
## Max. :1 Max. :1 Max. :0.9992 Max. :1 Max. :0.7375
##
## AccuracyPValue McnemarPValue Sensitivity Specificity Pos Pred Value
## Min. :0 Min. : NA Min. :1 Min. :1 Min. :1
## 1st Qu.:0 1st Qu.: NA 1st Qu.:1 1st Qu.:1 1st Qu.:1
## Median :0 Median : NA Median :1 Median :1 Median :1
## Mean :0 Mean :NaN Mean :1 Mean :1 Mean :1
## 3rd Qu.:0 3rd Qu.: NA 3rd Qu.:1 3rd Qu.:1 3rd Qu.:1
## Max. :0 Max. : NA Max. :1 Max. :1 Max. :1
## NA's :300
## Neg Pred Value Precision Recall F1 Prevalence
## Min. :1 Min. :1 Min. :1 Min. :1 Min. :0.7375
## 1st Qu.:1 1st Qu.:1 1st Qu.:1 1st Qu.:1 1st Qu.:0.7375
## Median :1 Median :1 Median :1 Median :1 Median :0.7375
## Mean :1 Mean :1 Mean :1 Mean :1 Mean :0.7375
## 3rd Qu.:1 3rd Qu.:1 3rd Qu.:1 3rd Qu.:1 3rd Qu.:0.7375
## Max. :1 Max. :1 Max. :1 Max. :1 Max. :0.7375
##
## Detection Rate Detection Prevalence Balanced Accuracy
## Min. :0.7375 Min. :0.7375 Min. :1
## 1st Qu.:0.7375 1st Qu.:0.7375 1st Qu.:1
## Median :0.7375 Median :0.7375 Median :1
## Mean :0.7375 Mean :0.7375 Mean :1
## 3rd Qu.:0.7375 3rd Qu.:0.7375 3rd Qu.:1
## Max. :0.7375 Max. :0.7375 Max. :1
##
Now, we add additional information about the optimal cutpoint
ft.g2p_cutp.dmps <- selectDIMP(ft.g2p.dmps, div.col = 9L, cutpoint = cut.g2p$cutpoint)
ft.g2p_cut.class = evaluateDIMPclass(LR = ft.g2p_cutp.dmps, control.names = control.nam,
treatment.names = treatment.nam,
column = c(hdiv = TRUE, TV = TRUE,
wprob = TRUE, pos = TRUE),
classifier = "pca.lda", n.pc = 4,
center = TRUE, scale = TRUE, num.boot = 300,
output = "all", prop = 0.6
)
ft.g2p_cut.class$mc.val
## Accuracy Kappa AccuracyLower AccuracyUpper AccuracyNull
## Min. :1 Min. :1 Min. :0.9991 Min. :1 Min. :0.9139
## 1st Qu.:1 1st Qu.:1 1st Qu.:0.9991 1st Qu.:1 1st Qu.:0.9139
## Median :1 Median :1 Median :0.9991 Median :1 Median :0.9139
## Mean :1 Mean :1 Mean :0.9991 Mean :1 Mean :0.9139
## 3rd Qu.:1 3rd Qu.:1 3rd Qu.:0.9991 3rd Qu.:1 3rd Qu.:0.9139
## Max. :1 Max. :1 Max. :0.9991 Max. :1 Max. :0.9139
##
## AccuracyPValue McnemarPValue Sensitivity Specificity Pos Pred Value
## Min. :9.096e-154 Min. : NA Min. :1 Min. :1 Min. :1
## 1st Qu.:9.096e-154 1st Qu.: NA 1st Qu.:1 1st Qu.:1 1st Qu.:1
## Median :9.096e-154 Median : NA Median :1 Median :1 Median :1
## Mean :9.096e-154 Mean :NaN Mean :1 Mean :1 Mean :1
## 3rd Qu.:9.096e-154 3rd Qu.: NA 3rd Qu.:1 3rd Qu.:1 3rd Qu.:1
## Max. :9.096e-154 Max. : NA Max. :1 Max. :1 Max. :1
## NA's :300
## Neg Pred Value Precision Recall F1 Prevalence
## Min. :1 Min. :1 Min. :1 Min. :1 Min. :0.9139
## 1st Qu.:1 1st Qu.:1 1st Qu.:1 1st Qu.:1 1st Qu.:0.9139
## Median :1 Median :1 Median :1 Median :1 Median :0.9139
## Mean :1 Mean :1 Mean :1 Mean :1 Mean :0.9139
## 3rd Qu.:1 3rd Qu.:1 3rd Qu.:1 3rd Qu.:1 3rd Qu.:0.9139
## Max. :1 Max. :1 Max. :1 Max. :1 Max. :0.9139
##
## Detection Rate Detection Prevalence Balanced Accuracy
## Min. :0.9139 Min. :0.9139 Min. :1
## 1st Qu.:0.9139 1st Qu.:0.9139 1st Qu.:1
## Median :0.9139 Median :0.9139 Median :1
## Mean :0.9139 Mean :0.9139 Mean :1
## 3rd Qu.:0.9139 3rd Qu.:0.9139 3rd Qu.:1
## Max. :0.9139 Max. :0.9139 Max. :1
##
In other words, information on the probability distributions of the natural
spontaneous methylation variation in the control and treatment population are
essential to discriminate the background noise from the treatment induced
signal.
Graphics of DMP classification performance
DMP count data:
dt <- t(rbind(G2P = sapply(g2p.dmps, length),
G3P = sapply(g3p.dmps, length),
FT = sapply(ft.dmps, length),
FT.G2P = sapply(ft.g2p.dmps, length),
FT.SD = sapply(ft.g2p_cutp.dmps, length)
))
dt
## G2P G3P FT FT.G2P FT.SD
## C1 255 251 1730 1055 255
## C2 306 298 1682 1070 306
## C3 281 276 1657 1059 281
## T1 2925 2871 7589 2926 2925
## T2 3032 2965 7646 3032 3032
## T3 2990 2934 7679 2990 2990
The comparison between the approaches FT.G2P and FT.SD (full signal detection on
FT output) tells us that only 255, 306, and 281 cytosine sites detected with FT
in the control samples C1, C2, and C3, respectively, carry methylation signals
comparable (in magnitude) to those signals induced by the treatment.
Classification performance data:
df <- data.frame(method = c("FT", "FT.G2P", "FT.SD", "G2P", "G3P"),
rbind(
c(colMeans(ft.class$boots)[c(1, 8:11, 18)], FDR = ft.class$con.mat$FDR),
c(colMeans(ft.g2p.class$boots)[c(1, 8:11, 18)], FDR = ft.g2p.class$con.mat$FDR),
c(colMeans(ft.g2p_cut.class$boots)[c(1, 8:11, 18)], FDR = ft.g2p_cut.class$con.mat$FDR),
c(colMeans(g2p.class$boots)[c(1, 8:11, 18)], FDR = g2p.class$con.mat$FDR),
c(colMeans(g3p.class$boots)[c(1, 8:11, 18)], FDR = g3p.class$con.mat$FDR)
))
Graphics:
color <- c("darkgreen", "#147714FF", "#3D9F3DFF", "#66C666FF", "#90EE90FF")
dt <- data.frame(dt, sample = names(g2p.dmps))
## ------------------------- DMP count graphic ---------------------------------
par(family = "serif", lwd = 0.1, cex = 1, mar = c(2,5,2,2), mfcol = c(1, 2))
barplot(cbind(FT, FT.G2P, FT.SD, G2P, G3P) ~ sample,
panel.first={points(0, 0, pch=16, cex=1e6, col="grey95")
grid(col="white", lty = 1, lwd = 1)},
data = dt, beside = TRUE, legend.text = TRUE, las = 1, lwd = 0.05, yaxt = "n",
cex.names = 1.4, font = 3, xlab = "", col = color,
args.legend = list(x=10, y=6000, text.font = 2, box.lwd = 0, horiz = FALSE,
adj = 0, xjust = 0.65, yjust = 0.8, bty = "n", cex = 1.2,
x.intersp = 0.2, inset = -1, ncol = 1, fill = color))
axis(2, hadj = 0.9, las = 2, lwd = 0.4, tck = -0.02, cex.axis = 1.2, font = 2, line = -0.2)
mtext(side = 2, text = "DMP count", line = 3, cex = 1.4, font = 3)
## ------------------ DMP classifiction performance graphic -------------------
color <- c("mediumblue", "#0000FFFF", "#3949F6FF", "#566CF2FF", "#7390EEFF", "#90B3EAFF", "#ADD8E6FF")
labs <- df$method
par(family = "serif", lwd = 0.1, cex = 1, mar = c(4,2,2,10))
x <- barplot(cbind(Accuracy, Sensitivity, Specificity, Pos.Pred.Value, Neg.Pred.Value,
Balanced.Accuracy, FDR) ~ method,
panel.first={points(0, 0, pch=16, cex=1e6, col="grey95")
grid(col="white", lty = 1, lwd = 1)},
data = df, beside = TRUE, legend.text = TRUE, las = 1, lwd = 0.1, yaxt = "n",
cex.names = 1.4, font = 3, xlab = "", col = color, ylim = c(0,1),
args.legend = list(x = 52, y = 1., text.font = 2, box.lwd = 0, horiz = FALSE,
adj = 0, xjust = 0.65, yjust = 0.8, bty = "n", cex = 1.2,
x.intersp = 0.2, inset = -1, ncol = 1, fill = color))
axis(2, hadj = 0.8, las = 2, lwd = 0.4, tck = -0.02, cex.axis = 1.2, font = 2,
line = -0.4)
mtext(side = 2, text = "Performance value", line = 2, cex = 1.4, font = 3)

FT.G2P and FT.SD approaches lead to excellent classification performances on this
data set. At this point, we can appeal the parsimony principle, follows from
Occam’s razor that states
“among competing hypotheses, the hypothesis with the fewest assumptions should
be selected. In other words, results indicates that the signal-detection and
machine-learning approach is sufficient [@ElNaqa2018; @Sanchez2019].
Conclusions
-
A proper discrimination of the methylation signal from the stochastic
methylation background requires for the knowledge of probability distributions
of the methylation signal from control and treatment population. Such a
knowledge permits a suitable estimation of the cutoff value to discriminate the
methylation signal induced by the treatment from the stochastic methylation
background detected in the control group.
-
It does not matter how significant a differentially methylation event for a
given cytosine position would be (after the application of some statistical
test), but on how big the probability to be observed in the control group is. In
simple words, if for a given DMP the probability of to be observed in the control
is big enough, then such a DMP did not result from a treatment effect.
-
A suitable evaluation on how much the mentioned probability can be big
enough derives by estimating an optimal cutpoint. But a classification into two
groups results from the cutpoint estimation and the problem on the estimation of
such a cutpoint is equivalent to find a discriminatory function (as set by
Fisher, [@Fisher1938; @Green1979]). Cases with function values below some cutoff
are classified in one group, while values above the cutoff are put in the other
group.
-
MethylIT function
estimateCutPoint
permits the estimation and search for an optimal cutpoint by confronting the
problem as in the spirit of the classical signal detection and as a
classification problem. The best model classifier will depend on the dataset
under study.So, uses must check for which is the model classifier with the best
classification performance for his/her dataset.
References
-
Ngo, Thuy T.M., Jejoong Yoo, Qing Dai, Qiucen Zhang, Chuan He, Aleksei Aksimentiev, and Taekjip Ha. 2016. “Effects of cytosine modifications on DNA flexibility and nucleosome mechanical stability.” Nature Communications 7 (February). Nature Publishing Group: 10813. https://doi.org/10.1038/ncomms10813.
-
Min, Wei, Liang Jiang, Ji Yu, S C Kou, Hong Qian, and X Sunney Xie. 2005. “Nonequilibrium steady state of a nanometric biochemical system: Determining the thermodynamic driving force from single enzyme turnover time traces.” Nano Letters 5 (12): 2373–8. https://doi.org/10.1021/nl0521773.
-
Koslover, Elena F, and Andrew J Spakowitz. 2012. “Force fluctuations impact kinetics of biomolecular systems.” Physical Review. E, Statistical, Nonlinear, and Soft Matter Physics 86 (1 Pt 1): 011906. http://www.ncbi.nlm.nih.gov/pubmed/23005451.
-
Samoilov, Michael S., Gavin Price, and Adam P. Arkin. 2006. “From fluctuations to phenotypes: the physiology of noise.” Science’s STKE : Signal Transduction Knowledge Environment 2006 (366). https://doi.org/10.1126/stke.3662006re17.
-
Eldar, Avigdor, and Michael B. Elowitz. 2010. “Functional roles for noise in genetic circuits.” Nature Publishing Group. https://doi.org/10.1038/nature09326.
-
Sanchez, Robersy, and Sally A. Mackenzie. 2016. “Information Thermodynamics of Cytosine DNA Methylation.” Edited by Barbara Bardoni. PLOS ONE 11 (3). Public Library of Science: e0150427. https://doi.org/10.1371/journal.pone.0150427.
-
Sanchez, Robersy, Xiaodong Yang, Thomas Maher, and Sally Mackenzie. 2019. “Discrimination of DNA Methylation Signal from Background Variation for Clinical Diagnostics.” Int. J. Mol. Sci. 20 (21): 5343. https://doi.org/https://doi.org/10.3390/ijms20215343.
-
Youden, W. J. 1950. “Index for rating diagnostic tests.” Cancer 3 (1): 32–35. https://doi.org/10.1002/1097-0142(1950)3:1<32::AID-CNCR2820030106>3.0.CO;2-3.
-
El Naqa, Issam, Dan Ruan, Gilmer Valdes, Andre Dekker, Todd McNutt, Yaorong Ge, Q. Jackie Wu, et al. 2018. “Machine learning and modeling: Data, validation, communication challenges.” Medical Physics 45 (10): e834–e840. https://doi.org/10.1002/mp.12811.
-
Fisher, R.A. 1938. “The statistical utilization of multiple measurents.” Annals of Eugenics 8: 376–86.
-
Green, Bert F. 1979. “The Two Kinds of Linear Discriminant Functions and Their Relationship.” Journal of Educational Statistics 4 (3): 247–63.