Robersy Sanchez
New horizons for genomic mathematics are glimpsed in the Post-Genomic Era. However, communication of the basic results on genomic mathematics to the scientific community not familiar with mathematical biology and to a wider audience is a challenge. We are living times in which there are so many interesting things to see and to learn that there is almost no time to discover the beauty of nature in those things that require the lens of mathematics to be observed.
The best is yet to come
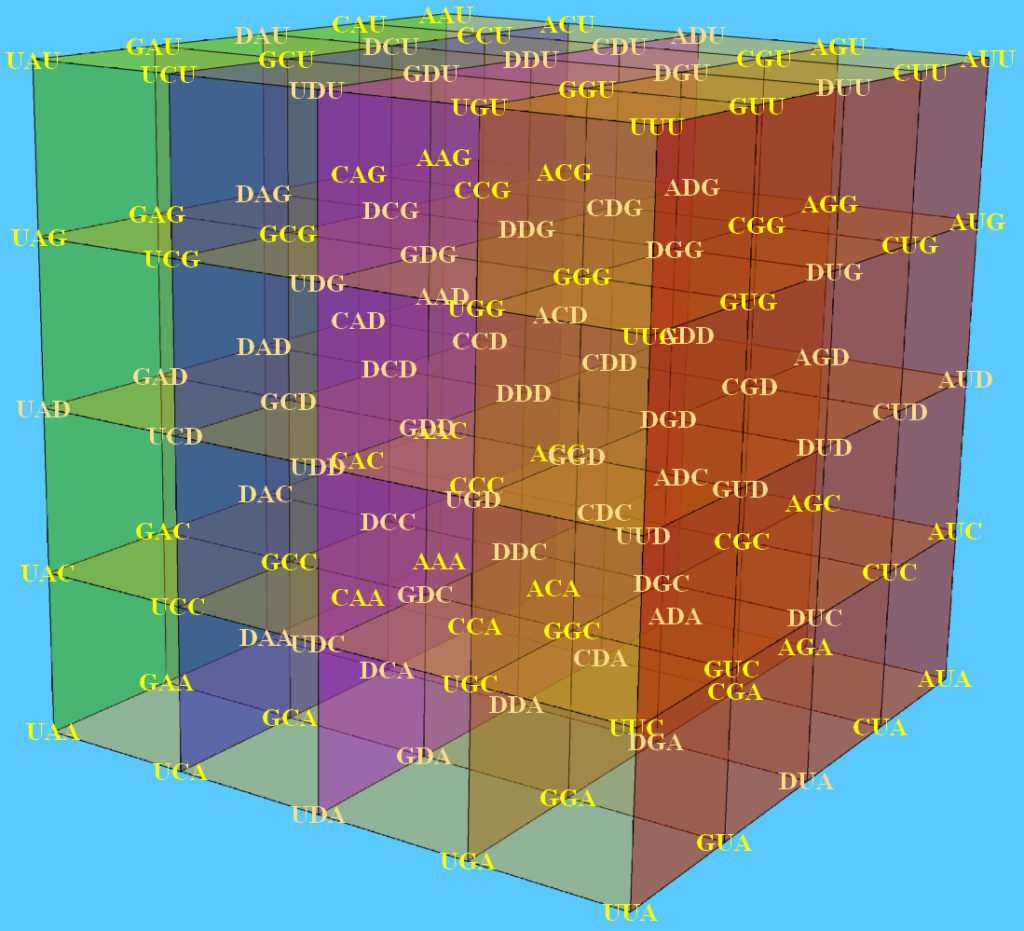
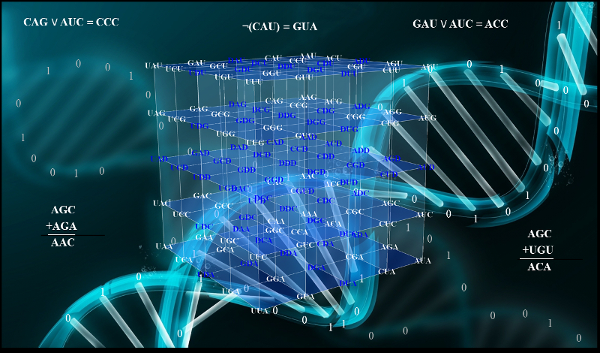
The genetic code is the cornerstone of life on earth, the fundamental set of biochemical rules that distinguish living organisms from non-living matter. The quantitative relationships between the DNA bases in the codons permit the description of the genetic code as a cube inserted in the three dimensional space.
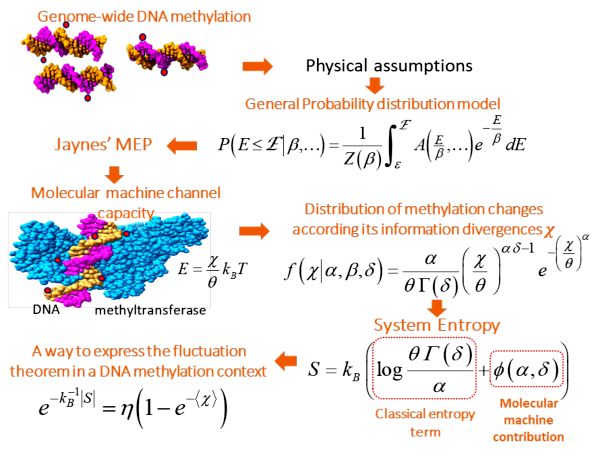
Information Thermodynamics of Cytosine DNA Methylation. Consistent with thermodynamic principles acting within living systems and the application of maximum entropy principle, we propose a theoretical framework to understand and decode the DNA methylation process.

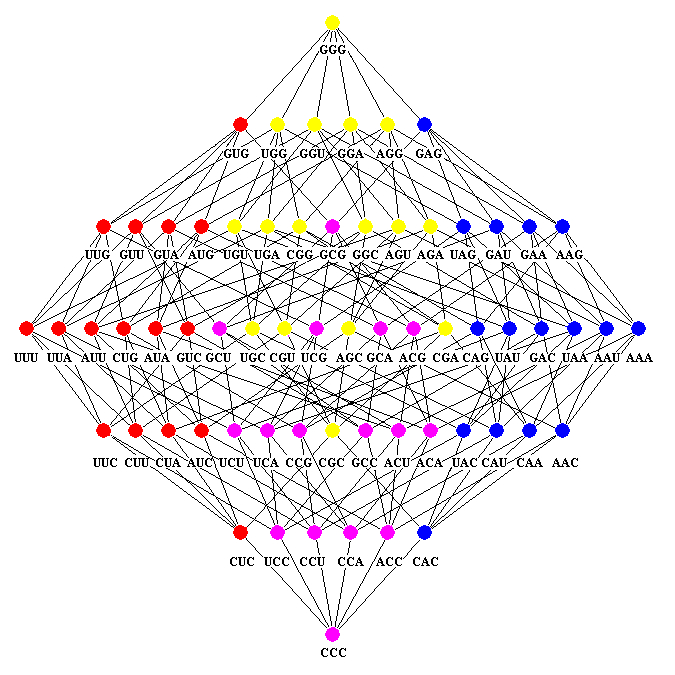
To know in advance the fixation probability of immune escape epitopes is essential to build successful vaccines. The fixation probabilities of mutational events on viral proteins can be estimated in a thermodynamics framework of the symmetric group of genetic-code cubes (get Computational Document Format (CDF) here)
GenomAutomorphism. This is a R package to compute the automorphisms between pairwise aligned DNA sequences represented as elements from a Genomic Abelian group as described in the paper Genomic Abelian Finite Groups.