On the DNA Computer Binary Code
In any finite set we can define a partial order, a binary operation in different ways. But here, a partial order is defined in the set of four DNA bases in such a manner that a Boolean lattice structure is obtained. A Boolean lattice is an algebraic structure that captures essential properties of both set operations and logic operations. This partial order is defined based on the physico-chemical properties of the DNA bases: hydrogen bond number and chemical type: of purine {A, G} and pyrimidine {U, C}. This physico-mathematical description permits the study of the genetic information carried by the DNA molecules as a computer binary code of zeros (0) and (1).
1. Boolean lattice of the four DNA bases
In any four-element Boolean lattice every element is comparable to every other, except two of them that are, nevertheless, complementary. Consequently, to build a four-base Boolean lattice it is necessary for the bases with the same number of hydrogen bonds in the DNA molecule and in different chemical types to be complementary elements in the lattice. In other words, the complementary bases in the DNA molecule (G≡C and A=T or A=U during the translation of mRNA) should be complementary elements in the Boolean lattice. Thus, there are four possible lattices, each one with a different base as the maximum element.
2. Boolean (logic) operations in the set of DNA bases
The Boolean algebra on the set of elements X will be denoted by $(B(X), \vee, \wedge)$. Here the operators $\vee$ and $\wedge$ represent classical “OR” and “AND” logical operations term-by-term. From the Boolean algebra definition it follows that this structure is (among other things) a partially ordered set in which any two elements $\alpha$ and $\beta$ have upper and lower bounds. Particularly, the greater lower bound of the elements $\alpha$ and $\beta$ is the element $\alpha\vee\beta$ and the least upper bound is the element $\alpha\wedge\beta$. This equivalent partial ordered set is called Boolean lattice.
- In every Boolean algebra (denoted by $(B(X), \vee, \wedge)$) for any two elements , $\alpha,\beta \in X$ we have $\alpha \le \beta$, if and only if $\neg\alpha\vee\beta=1$, where symbol “$\neg$” stands for the logic negation. If the last equality holds, then it is said that $\beta$ is deduced from $\alpha$. Furthermore, if $\alpha \le \beta$ or $\alpha \ge \beta$ the elements and are said to be comparable. Otherwise, they are said not to be comparable.
In the set of four DNA bases, we can built twenty four isomorphic Boolean lattices [1]. Herein, we focus our attention that one described in reference [2], where the DNA bases G and C are taken as the maximum and minimum elements, respectively, in the Boolean lattice. The logic operation in this DNA computer code are given in the following table:
| OR | AND | ||||||||
| $\vee$ | G | A | U | C | $\wedge$ | G | A | U | C |
| G | G | A | U | Ç | G | G | G | G | G |
| A | A | A | C | C | A | G | A | G | A |
| U | U | C | U | C | U | G | G | U | U |
| C | C | C | C | C | C | G | A | U | C |
It is well known that all Boolean algebras with the same number of elements are isomorphic. Therefore, our algebra $(B(X), \vee, \wedge)$ is isomorphic to the Boolean algebra $(\mathbb{Z}_2^2(X), \vee, \wedge)$, where $\mathbb{Z}_2 = \{0,1\}$. Then, we can represent this DNA Boolean algebra by means of the correspondence: $G \leftrightarrow 00$; $A \leftrightarrow 01$; $U \leftrightarrow 10$; $C \leftrightarrow 11$. So, in accordance with the operation table:
- $A \vee U = C \leftrightarrow 01 \vee 10 = 11$
- $U \wedge G = U \leftrightarrow 10 \wedge 00 = 00$
- $G \vee C = C \leftrightarrow 00 \vee 11 = 11$
The logic negation ($\neg$) of a base yields the DNA complementary base: $\neg A = U \leftrightarrow \neg 01 = 10$; $\neg G = C \leftrightarrow \neg 00 = 11$
- A Boolean lattice has in correspondence a directed graph called Hasse diagram, where two nodes (elements) $\alpha$ and $\beta$ are connected with a directed edge from $\alpha$ to $\beta$ (or connected with a directed edge from $\beta$ to $\alpha$) if, and only if, $\alpha \le \beta$ ($\alpha \ge \beta$) and there is no other element between $\alpha$ and $\beta$.
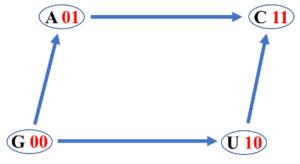
The figure shows the Hasse diagram corresponding to the Boolean algebra $(B(X), \vee, \wedge)$. There are twenty four possible Hasse diagrams of four DNA bases and they integrate a symmetric group isomorphic to the symmetric group of degree four $S_4$ [1].
3. The Genetic code Boolean Algebras
Boolean algebras of codons are, explicitly, derived as the direct product $C(X) = B(X) \times B(X) \times B(X)$. These algebras are isomorphic to the dual Boolean algebras $(\mathbb{Z}_2^6, \vee, \wedge)$ and $(\mathbb{Z}_2^6, \wedge, \vee)$ induced by the isomorphism $B(X) \cong \mathbb{Z}_2^2$, where $X$ runs over the twenty four possibles ordered sets of four DNA bases [1]. For example:
CAG $\vee$ AUC = CCC $\leftrightarrow$ 110100 $\vee$ 011011 = 111111
ACG $\wedge$ UGA = GGG $\leftrightarrow$ 011100 $\wedge$ 100001 = 000000
$\neg$ (CAU) = GUA $\leftrightarrow$ $\neg$ (110110) = 001001
The Hasse diagram for the corresponding Boolean algebra derived from the direct product of the Boolean algebra of four DNA bases given in the above operation table is:

In the Hasse diagram, chains and anti-chains are located. A Boolean lattice subset is called a chain if any two of its elements are comparable but, on the contrary, if any two of its elements are not comparable, the subset is called an anti-chain. In the Hasse diagram of codons shown in the figure, all chains with maximal length have the same minimum element GGG and the maximum element CCC. It is evident that two codons are in the same chain with maximal length if and only if they are comparable, for example the chain: GGG $\leftrightarrow$ GAG $\leftrightarrow$ AAG $\leftrightarrow$ AAA $\leftrightarrow$ AAC $\leftrightarrow$ CAC $\leftrightarrow$ CCC
The Hasse diagram symmetry reflects the role of hydrophobicity in the distribution of codons assigned to each amino acid. In general, codons that code to amino acids with extreme hydrophobic differences are in different chains with maximal length. In particular, codons with U as a second base will appear in chains of maximal length whereas codons with A as a second base will not. For that reason, it will be impossible to obtain hydrophobic amino acid with codons having U in the second position through deductions from hydrophilic amino acids with codons having A in the second position.
There are twenty four Hasse diagrams of codons, corresponding to the twenty four genetic-code Boolean algebras. These algebras integrate a symmetric group isomorphic to the symmetric group of degree four $S_4$ [1]. In summary, the DNA binary code is not arbitrary, but subject to logic operations with subjacent biophysical meaning.
References
- Sanchez R. Symmetric Group of the Genetic-Code Cubes. Effect of the Genetic-Code Architecture on the Evolutionary Process. MATCH Commun Math Comput Chem, 2018, 79:527–60.
- Sánchez R, Morgado E, Grau R. A genetic code Boolean structure. I. The meaning of Boolean deductions. Bull Math Biol, 2005, 67:1–14.