A Short Introduction to Algebraic Taxonomy on Genes Regions¶
Overview¶
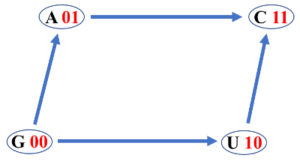
GenomAutomorphism is a R package to compute the autimorphisms between pairwise aligned DNA sequences represented as elements from a Genomic Abelian group as described in reference (1). In a general scenario, whole chromosomes or genomic regions from a population (from any species or close related species) can be algebraically represented as a direct sum of cyclic groups or more specifically Abelian p-groups. Basically, we propose the representation of multiple sequence alignments (MSA) of length N as a finite Abelian group created by the direct sum of Abelian group of prime-power order:
$\qquad G = (\mathbb{Z}_{p^{\alpha_{1}}_1})^{n_1} \oplus (\mathbb{Z}_{p^{\alpha_{2}}_1})^{n_2} \oplus \dots \oplus (\mathbb{Z}_{p^{\alpha_{k}}_k})^{n_k}$Where, the $p_i$’s are prime numbers, $\alpha_i \in \mathbb{N}$ and $\mathbb{Z}_{p^{\alpha_{i}}_i}$ is the group of integer modulo $p^{\alpha_{i}}_i$.
For the purpose of estimating the automorphism between two aligned DNA sequences, $p^{\alpha_{i}}_i \in \{5, 2^6, 5^3 \}$.
Automorphisms¶
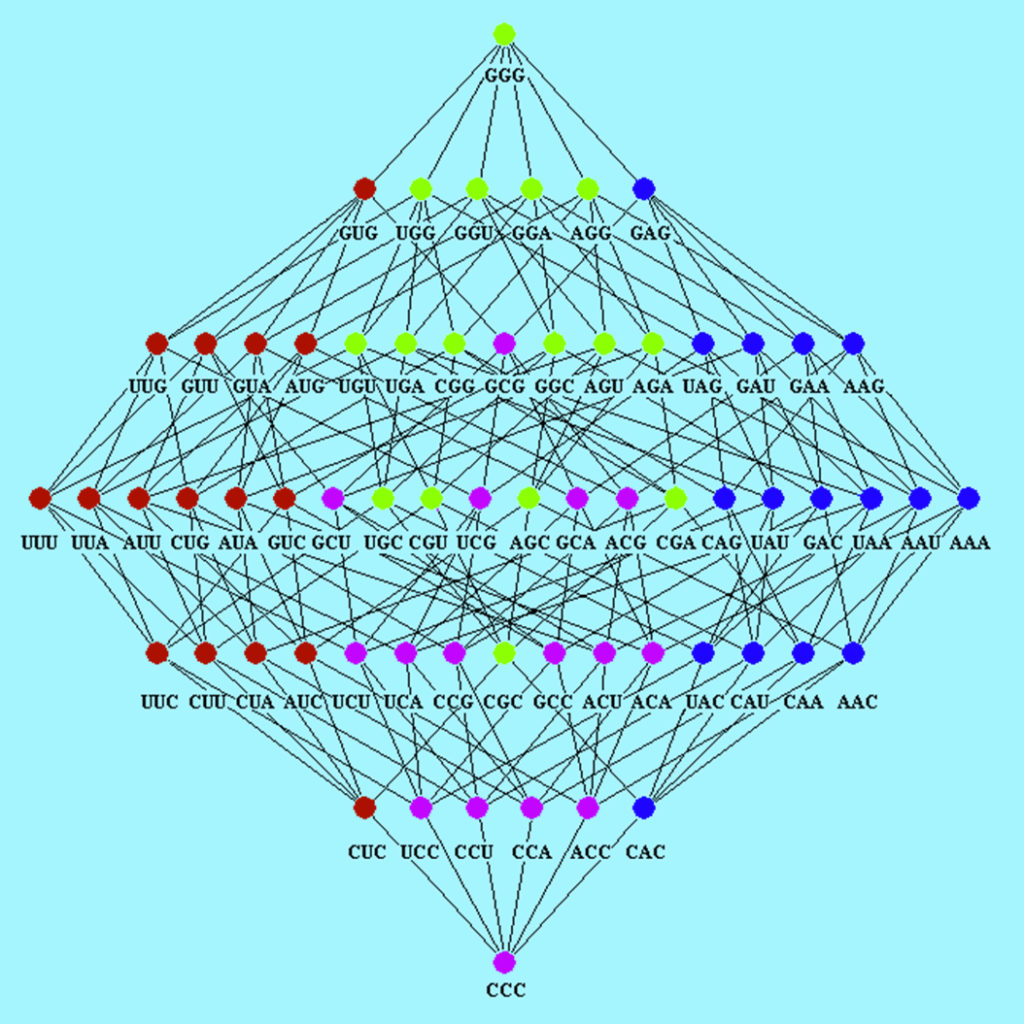
Herein, automorphisms are considered algebraic descriptions of mutational event observed in codon sequences represented on different Abelian groups. In particular, as described in references (3-4), for each representation of the codon set on a defined Abelian group there are 24 possible isomorphic Abelian groups. These Abelian groups can be labeled based on the DNA base-order used to generate them. The set of 24 Abelian groups can be described as a group isomorphic to the symmetric group of degree four ($S_4$, see reference (4)).
For further support about the symmetric group on the 24 Abelian group of genetic-code cubes, users can also see Symmetric Group of the Genetic-Code Cubes., specifically the Mathematica notebook IntroductionToZ5GeneticCodeVectorSpace.nb and interact with it using Wolfram Player, freely available (for Windows and Linux OS) at, https://www.wolfram.com/player/. Tutorials on how to use GenomAutomorphism in the analysis of mutational events are available at its website: https://genomaths.github.io/genomautomorphism/. The source package is available in GitHub at: https://github.com/genomaths/GenomAutomorphism/.
Automorphisms on $\mathbb{Z}_{64}$¶
First, we proceed to load or install, if needed, the R packages required for our analysis. If needed the R package required for the current analysis can be installed as:
In particular, you might require to install the library CHAID can be installed typing in R console:
install.packages(c("party", "partykit", "data.table", "ggplot2", "ggparty", "dplyr"), dependencies=TRUE)
In particular, you might require to install the library CHAID can be installed typing in R console:
install.packages("CHAID", repos="http://R-Forge.R-project.org")
You can install GenomAutomorphism package from GitHub
devtools::install_git("https://github.com/genomaths/GenomAutomorphism.git")
If all the required libraries all installed, then we proceed to load the libraries
library(GenomAutomorphism)
library(Biostrings)
library(party)
library(partykit)
library(data.table)
library(ggplot2)
library(ggparty)
library(dplyr)
library(CHAID)
Next, we proceed to check the DNA multiple sequence alignment (MSA) file. This is a FASTA file carrying the MSA of primate BRCA1 DNA repair gene. Notice that we are familiar with the FASTA file, then it is better to directly read it with function automorphism. However, for the current example, this step can be bypassed, since the MSA is provided provided together with GenomAutomorphism R package
## Do not run it. This is included with package
URL <- paste0("https://github.com/genomaths/seqalignments/raw/master/BRCA1/",
"brca1_primates_dna_repair_20_sequences.fasta")
brca1_aln <- readDNAMultipleAlignment(filepath = URL)
Load MSA available in the package
data("brca1_aln", package = "GenomAutomorphism")
brca1_aln
DNAMultipleAlignment with 20 rows and 2283 columns
aln names
[1] ATGGATTTATCTGCTCTTCGCGTTG...CCAGATCCCCCACAGCCACTACTGA NM_007298.3:20-22...
[2] ATGGATTTATCTGCTCTTCGCGTTG...CCAGATCCCCCACAGCCACTACTGA U64805.1:1-2280_H...
[3] ATGGATTTATCTGCTCTTCGCGTTG...CCAGATCCCCCACAGCCACTACTGA XM_031011560.1:23...
[4] ATGGATTTATCTGCTCTTCGCGTTG...CCAGATCCCCCACAGCCACTACTGA XM_031011561.1:23...
[5] ATGGATTTATCTGCTCTTCGCGTTG...CCAGATCCCCCACAGCCACTACTGA XM_031011562.1:16...
[6] ATGGATTTATCTGCTCTTCGCGTTG...TCAGATCCCCCACAGCCACTACTGA XM_009432101.3:27...
[7] ATGGATTTATCTGCTCTTCGCGTTG...TCAGATCCCCCACAGCCACTACTGA XM_009432104.3:37...
[8] ATGGATTTATCTGCTCTTCGCGTTG...TCAGATCCCCCACAGCCACTACTGA XM_016930487.2:37...
[9] ATGGATTTATCTGCTCTTCGCGTTG...TCAGATCCCCCACAGCCACTACTGA XM_009432099.3:37...
... ...
[12] ATGGATTTATCTGCTCTTCGCGTTG...TCAGATCCCCCACAGCCACTACTGA XM_034941185.1:24...
[13] ATGGATTTATCTGCTCTTCGCGTTG...TCAGATCCCCCACAGCCACTACTGA XM_034941182.1:25...
[14] ATGGATTTATCTGCTGTTCGCGTTG...CCAGATCCCCCACAGCCACTACTGA XM_032163757.1:14...
[15] ATGGATTTATCTGCTGTTCGCGTTG...CCAGATCCCCCACAGCCACTACTGA XM_032163756.1:14...
[16] ATGGATTTATCTGCTGTTCGCGTTG...CCAGATCCCCCACAGCCACTACTGA XM_032163758.1:13...
[17] ATGGATTTATCTGCTCTTCGCGTTG...CCAGATCCCCCACAGCCACTACTGA XM_030923119.1:18...
[18] ATGGATTTATCTGCTCTTCGCGTTG...CCAGATCCCCCACAGCCACTACTGA XM_030923118.1:18...
[19] ATGGATTTACCTGCTGTTCGCGTTG...CCAGATCCCCCACAGCCACTACTGA XM_025363316.1:14...
[20] ATGGATTTATCTGCTGTTCGTGTTG...CCAGATCCCTCACAGCCACTACTGA XM_039475995.1:49...
The sequence names
strtrim(names(brca1_aln@unmasked), 100)
- ‘NM_007298.3:20-2299_Homo_sapiens_BRCA1_DNA_repair_associated_(BRCA1)_transcript_variant_4_mRNA’
- ‘U64805.1:1-2280_Homo_sapiens_Brca1-delta11b_(Brca1)_mRNA_complete_cds’
- ‘XM_031011560.1:233-2515_PREDICTED:_Gorilla_gorilla_gorilla_BRCA1_DNA_repair_associated_(BRCA1)_trans’
- ‘XM_031011561.1:233-2512_PREDICTED:_Gorilla_gorilla_gorilla_BRCA1_DNA_repair_associated_(BRCA1)_trans’
- ‘XM_031011562.1:163-2442_PREDICTED:_Gorilla_gorilla_gorilla_BRCA1_DNA_repair_associated_(BRCA1)_trans’
- ‘XM_009432101.3:276-2555_PREDICTED:_Pan_troglodytes_BRCA1_DNA_repair_associated_(BRCA1)_transcript_va’
- ‘XM_009432104.3:371-2650_PREDICTED:_Pan_troglodytes_BRCA1_DNA_repair_associated_(BRCA1)_transcript_va’
- ‘XM_016930487.2:371-2650_PREDICTED:_Pan_troglodytes_BRCA1_DNA_repair_associated_(BRCA1)_transcript_va’
- ‘XM_009432099.3:371-2653_PREDICTED:_Pan_troglodytes_BRCA1_DNA_repair_associated_(BRCA1)_transcript_va’
- ‘XM_034941183.1:254-2533_PREDICTED:_Pan_paniscus_BRCA1_DNA_repair_associated_(BRCA1)_transcript_varia’
- ‘XM_034941184.1:254-2533_PREDICTED:_Pan_paniscus_BRCA1_DNA_repair_associated_(BRCA1)_transcript_varia’
- ‘XM_034941185.1:248-2527_PREDICTED:_Pan_paniscus_BRCA1_DNA_repair_associated_(BRCA1)_transcript_varia’
- ‘XM_034941182.1:254-2536_PREDICTED:_Pan_paniscus_BRCA1_DNA_repair_associated_(BRCA1)_transcript_varia’
- ‘XM_032163757.1:145-2418_PREDICTED:_Hylobates_moloch_BRCA1_DNA_repair_associated_(BRCA1)_transcript_v’
- ‘XM_032163756.1:145-2421_PREDICTED:_Hylobates_moloch_BRCA1_DNA_repair_associated_(BRCA1)_transcript_v’
- ‘XM_032163758.1:139-2412_PREDICTED:_Hylobates_moloch_BRCA1_DNA_repair_associated_(BRCA1)_transcript_v’
- ‘XM_030923119.1:184-2463_PREDICTED:_Rhinopithecus_roxellana_BRCA1_DNA_repair_associated_(BRCA1)_trans’
- ‘XM_030923118.1:183-2465_PREDICTED:_Rhinopithecus_roxellana_BRCA1_DNA_repair_associated_(BRCA1)_trans’
- ‘XM_025363316.1:147-2426_PREDICTED:_Theropithecus_gelada_BRCA1_DNA_repair_associated_(BRCA1)_transcri’
- ‘XM_039475995.1:49-2328_PREDICTED:_Saimiri_boliviensis_boliviensis_BRCA1_DNA_repair_associated_(BRCA1’
Next, function automorphism will be applied to represent the codon sequence in the Abelian group $\mathbb{Z}_{64}$ (i.e., the set of integers remainder modulo 64). The codon coordinates are requested on the cube ACGT. Following reference (4)), cubes are labeled based on the order of DNA bases used to define the sum operation.
In Z64, automorphisms are described as functions $f(x) = k\,x \quad mod\,64$, where $k$ and $x$ are elements from the set of integers modulo 64. Below, in function automorphism three important arguments are given values: group = “Z64”, cube = c(“ACGT”, “TGCA”), and _cubealt = c(“CATG”, “GTAC”). Setting for group specifies on which group the automorphisms will be computed. These groups can be: “Z5”, “Z64”, “Z125”, and “Z5^3”.
In groups “Z64” and “Z125” not all the mutational events can be described as automorphisms from a given cube. So, a character string denoting pairs of “dual” the genetic-code cubes, as given in references (1-4)), is given as argument for cube. That is, the base pairs from the given cubes must be complementary each other. Such a cube pair are call dual cubes and, as shown in reference (4)), each pair integrates group. If automorphisms are not found in first set of dual cubes, then the algorithm search for automorphism in a alternative set of dual cubes.
## Do not run it. This is included with package
nams <- c("human_1","human_2","gorilla_1","gorilla_2","gorilla_3",
"chimpanzee_1","chimpanzee_2","chimpanzee_3","chimpanzee_4",
"bonobos_1","bonobos_2","bonobos_3","bonobos_4","silvery_gibbon_1",
"silvery_gibbon_1","silvery_gibbon_3","golden_monkey_1",
"golden_monkey_2","gelada_baboon","bolivian_monkey")
brca1_autm <- automorphism(
seqs = brca1_aln,
group = "Z64",
cube = c("ACGT", "TGCA"),
cube_alt = c("CATG", "GTAC"),
nms = nams,
verbose = FALSE)
Object brca1_autm is included with package and can be load typing:
data(brca1_autm, package = "GenomAutomorphism")
brca1_autm
AutomorphismList object of length: 190
names(190): human_1.human_2 human_1.gorilla_1 human_1.gorilla_2 ... golden_monkey_2.gelada_baboon golden_monkey_2.bolivian_monkey gelada_baboon.bolivian_monkey
-------
Automorphism object with 761 ranges and 6 metadata columns:
seqnames ranges strand | seq1 seq2 coord1 coord2
<Rle> <IRanges> <Rle> | <character> <character> <numeric> <numeric>
[1] 1 1 + | ATG ATG 50 50
[2] 1 2 + | GAT GAT 11 11
[3] 1 3 + | TTA TTA 60 60
[4] 1 4 + | TCT TCT 31 31
[5] 1 5 + | GCT GCT 27 27
... ... ... ... . ... ... ... ...
[757] 1 757 + | CAC CAC 5 5
[758] 1 758 + | AGC AGC 33 33
[759] 1 759 + | CAC CAC 5 5
[760] 1 760 + | TAC TAC 13 13
[761] 1 761 + | TGA TGA 44 44
autm cube
<numeric> <character>
[1] 1 ACGT
[2] 1 ACGT
[3] 1 ACGT
[4] 1 ACGT
[5] 1 ACGT
... ... ...
[757] 1 ACGT
[758] 1 ACGT
[759] 1 ACGT
[760] 1 ACGT
[761] 1 ACGT
-------
seqinfo: 1 sequence from an unspecified genome; no seqlengths
...
<189 more DFrame element(s)>
Two slots: 'DataList' & 'SeqRanges'
-------
Grouping automorphism by automorphism’s coefficients¶
Automorphisms with the same automorphism’s coefficients can be grouped. This task can be accomplished with function automorphismByCoef. However, for the sake of time, its output is included in the package.
## Not need to run it here
autby_coef <- automorphismByCoef(x = brca1_autm,
verbose = FALSE)
Object brca1_autm is included with package and can be load typing:
data(autby_coef, package = "GenomAutomorphism")
autby_coef
AutomorphismByCoefList object of length 190:
$human_1.human_2
AutomorphismByCoef object with 239 ranges and 5 metadata columns:
seqnames ranges strand | seq1 seq2 autm
<Rle> <IRanges> <Rle> | <character> <character> <numeric>
[1] 1 1-238 + | ATG ATG 1
[2] 1 1-238 + | GAT GAT 1
[3] 1 1-238 + | TTA TTA 1
[4] 1 1-238 + | TCT TCT 1
[5] 1 1-238 + | GCT GCT 1
... ... ... ... . ... ... ...
[235] 1 511-761 + | CCC CCC 1
[236] 1 511-761 + | CTT CTT 1
[237] 1 511-761 + | CCT CCT 1
[238] 1 511-761 + | ATA ATA 1
[239] 1 511-761 + | TGA TGA 1
mut_type cube
<character> <character>
[1] HHH ACGT
[2] HHH ACGT
[3] HHH ACGT
[4] HHH ACGT
[5] HHH ACGT
... ... ...
[235] HHH ACGT
[236] HHH ACGT
[237] HHH ACGT
[238] HHH ACGT
[239] HHH ACGT
-------
seqinfo: 1 sequence from an unspecified genome; no seqlengths
...
<189 more elements>
In the next, we are interested on mutational events in respect to human (as reference).
nams <- names(brca1_autm)
idx1 <- grep("human_1.", nams)
idx2 <- grep("human_2.", nams)
idx <- union(idx1, idx2)
h_brca1_autm <- unlist(brca1_autm[ idx ])
h_brca1_autm = h_brca1_autm[ which(h_brca1_autm$autm != 1) ]
h_brca1_autm
Automorphism object with 1397 ranges and 6 metadata columns:
seqnames ranges strand | seq1 seq2
<Rle> <IRanges> <Rle> | <character> <character>
human_1.human_2 1 239 + | CAT CGT
human_1.human_2 1 253 + | GCA GTA
human_1.human_2 1 323 + | TCT CCT
human_1.human_2 1 333 + | TCT TCC
human_1.human_2 1 350 + | --- ---
... ... ... ... . ... ...
human_2.bolivian_monkey 1 716 + | AAT AGT
human_2.bolivian_monkey 1 726 + | GAG GAA
human_2.bolivian_monkey 1 730 + | GTG GTA
human_2.bolivian_monkey 1 731 + | ACC ACT
human_2.bolivian_monkey 1 756 + | CCC CCT
coord1 coord2 autm cube
<numeric> <numeric> <numeric> <character>
human_1.human_2 7 39 33 ACGT
human_1.human_2 24 56 21 ACGT
human_1.human_2 31 23 9 ACGT
human_1.human_2 31 29 3 ACGT
human_1.human_2 NA NA -1 Gaps
... ... ... ... ...
human_2.bolivian_monkey 3 35 33 ACGT
human_2.bolivian_monkey 10 8 52 ACGT
human_2.bolivian_monkey 58 56 12 ACGT
human_2.bolivian_monkey 17 19 35 ACGT
human_2.bolivian_monkey 21 23 59 ACGT
-------
seqinfo: 1 sequence from an unspecified genome; no seqlengths
Bar plot automorphism distribution by coefficient¶
The automorphism distribution by cubes can be summarized in the bar-plot graphic.
Object autby_coef carried all the pairwise comparisons, while it will be enough to use data from a single species as reference, e.g., humans.
First the data must be reordered into a data.frame object:
h_autby_coef <- automorphismByCoef(x = h_brca1_autm)
h_autby_coef
AutomorphismByCoef object with 1395 ranges and 5 metadata columns:
seqnames ranges strand | seq1 seq2
<Rle> <IRanges> <Rle> | <character> <character>
human_1.gelada_baboon 1 4 + | TCT CCT
human_2.gelada_baboon 1 4 + | TCT CCT
human_1.silvery_gibbon_1 1 6 + | CTT GTT
human_1.silvery_gibbon_1 1 6 + | CTT GTT
human_1.silvery_gibbon_3 1 6 + | CTT GTT
... ... ... ... . ... ...
human_2.bonobos_2 1 753 + | CCC CCT
human_2.bonobos_3 1 753 + | CCC CCT
human_2.bonobos_4 1 753 + | CCC CCT
human_1.bolivian_monkey 1 756 + | CCC CCT
human_2.bolivian_monkey 1 756 + | CCC CCT
autm mut_type cube
<numeric> <character> <character>
human_1.gelada_baboon 9 YHH ACGT
human_2.gelada_baboon 9 YHH ACGT
human_1.silvery_gibbon_1 29 SHH ACGT
human_1.silvery_gibbon_1 29 SHH ACGT
human_1.silvery_gibbon_3 29 SHH ACGT
... ... ... ...
human_2.bonobos_2 59 HHY ACGT
human_2.bonobos_3 59 HHY ACGT
human_2.bonobos_4 59 HHY ACGT
human_1.bolivian_monkey 59 HHY ACGT
human_2.bolivian_monkey 59 HHY ACGT
-------
seqinfo: 1 sequence from an unspecified genome; no seqlengths
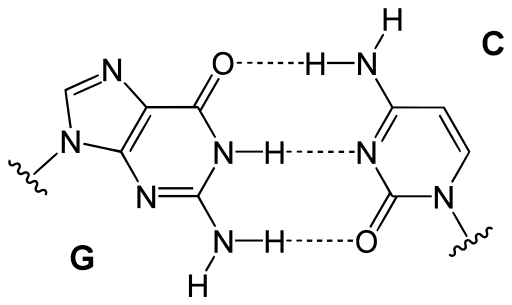
Every single base mutational event across the MSA was classified according IUPAC nomenclature: 1) According to the number of hydrogen bonds (on DNA/RNA double helix): strong S={C, G} (three hydrogen bonds) and weak W={A, U} (two hydrogen bonds). According to the chemical type: purines R={A, G} and pyrimidines Y={C, U}. 3). According to the presence of amino or keto groups on the base rings: amino M={C, A} and keto K={G, T}. Constant (hold) base positions were labeled with letter H. So, codon positions labeled as HKH means that the first and third bases remains constant and mutational events between bases G and T were found in the MSA.
nams <- names(h_autby_coef)
nams <- sub("human[_][1-2][.]", "", nams)
nams <- sub("[_][1-6]", "", nams)
dt <- data.frame(h_autby_coef, species = nams)
dt <- data.frame(dt, species = nams)
dt <- dt[, c("start", "autm", "species", "mut_type", "cube")]
DataFrame(dt)
DataFrame with 1395 rows and 5 columns
start autm species mut_type cube
<integer> <numeric> <character> <character> <character>
1 4 9 gelada_baboon YHH ACGT
2 4 9 gelada_baboon YHH ACGT
3 6 29 silvery_gibbon SHH ACGT
4 6 29 silvery_gibbon SHH ACGT
5 6 29 silvery_gibbon SHH ACGT
... ... ... ... ... ...
1391 753 59 bonobos HHY ACGT
1392 753 59 bonobos HHY ACGT
1393 753 59 bonobos HHY ACGT
1394 756 59 bolivian_monkey HHY ACGT
1395 756 59 bolivian_monkey HHY ACGT
Nominal variables are transformed into factor
dt$start <- as.numeric(dt$start)
dt$autm <- as.numeric(dt$autm)
dt$cube <- as.factor(dt$cube)
dt$species <- as.factor(dt$species)
dt$mut_type <- as.factor(dt$mut_type)
Finally the bar-plot is built typing:
counts <- table(dt$cube)
par(family = "serif", cex = 1, font = 2, mar=c(4,6,4,4))
barplot(counts, #main="Automorphism distribution",
xlab="Genetic-code cube representation",
ylab="Fixed mutational events",
col=c("darkblue","red", "darkgreen", "magenta", "orange"),
border = NA, axes = F, #ylim = c(0, 6000),
cex.lab = 2, cex.main = 1.5, cex.names = 2)
axis(2, at = c(0, 200, 400, 600, 800, 1000), cex.axis = 1.5)
mtext(side = 1,line = -3, at = c(0.7, 1.9, 3.1, 4.3),
text = paste0( counts ), cex = 2,
col = c("white", "red","yellow", "black"))
Classification Tree Chi-squared Automated Interaction Detection (CHAID)¶
The current CHAID implementation only accepts nominal or ordinal categorical predictors. When predictors are continuous, they have to be transformed into ordinal predictors before using the following algorithm. We create a ordinal variable autms from variable autm. The variables of interest are defined and encoded.
interval <- function(x, a, b) {
x >= a & x <= b
}
datos = dt
datos$autms <- case_when(datos$autm < 16 ~ 'A1',
interval(datos$autm, 16, 31) ~ 'A2',
interval(datos$autm, 32, 47) ~ 'A3',
datos$autm > 47 ~ 'A4')
datos$autms <- as.factor(datos$autms)
datos$mut_type <- as.character(datos$mut_type)
datos$mut_type[ which(datos$cube == "Trnl") ] <- "indel"
datos$mut_type[ which(datos$cube == "Gaps") ] <- "---"
datos$mut_type <- as.factor(datos$mut_type)
datos$regions <- case_when(datos$start < 230 ~ 'R0',
interval(datos$start, 230, 270) ~ 'R1',
interval(datos$start, 271, 305) ~ 'R2',
interval(datos$start, 306, 338) ~ 'R3',
interval(datos$start, 339, 533) ~ 'R4',
interval(datos$start, 534, 570) ~ 'R5',
interval(datos$start, 571, 653) ~ 'R6',
interval(datos$start, 654, 709) ~ 'R7',
datos$start > 709 ~ 'R8')
datos$regions <- as.factor(datos$regions)
datos$autm <- as.factor(datos$autm)
datos$species <- as.factor(datos$species)
datos$start <- as.factor(datos$start)
datos$cube <- as.factor(datos$cube)
datos <- datos[, c( "autms", "regions", "mut_type", "cube", "species")]
DataFrame(datos)
DataFrame with 1395 rows and 5 columns
autms regions mut_type cube species
<factor> <factor> <factor> <factor> <factor>
1 A1 R0 YHH ACGT gelada_baboon
2 A1 R0 YHH ACGT gelada_baboon
3 A2 R0 SHH ACGT silvery_gibbon
4 A2 R0 SHH ACGT silvery_gibbon
5 A2 R0 SHH ACGT silvery_gibbon
... ... ... ... ... ...
1391 A4 R8 HHY ACGT bonobos
1392 A4 R8 HHY ACGT bonobos
1393 A4 R8 HHY ACGT bonobos
1394 A4 R8 HHY ACGT bolivian_monkey
1395 A4 R8 HHY ACGT bolivian_monkey
A classification tree is estimated with CHAID algorithm:
ctrl <- chaid_control(minsplit = 200, minprob = 0.8, alpha2 = 0.01, alpha4 = 0.01)
chaid_res <- chaid(species ~ autms + regions + mut_type + cube , data = datos,
control = ctrl)
## Updating CHAID decision tree
dp <- data_party(chaid_res)
dat <- dp[, c("autms", "regions", "mut_type", "cube")]
dat$species <- dp[, "(response)"]
chaid_tree <- party(node = node_party(chaid_res),
data = dat,
fitted = dp[, c("(fitted)", "(response)")],
names = names(chaid_res))
## Extract p-values
pvals <- unlist(nodeapply(chaid_tree, ids = nodeids(chaid_tree), function(n) {
pvals <- info_node(n)$adjpvals
pvals < pvals[ which.min(pvals) ]
return(pvals)
}))
pvals <- pvals[ pvals < 0.05 ]
## Counts of event per spciees on each node
node.freq <- sapply(seq_along(chaid_tree), function(id) {
y <- data_party(chaid_tree, id = id)
y <- y[[ "(response)" ]]
table(y)
})
## total counts on each
node.size = colSums(node.freq)
Plotting the tree with ggparty (font size adjusted for html output)
options(repr.plot.width = 24, repr.plot.height = 20)
ggparty(chaid_tree) +
geom_edge(aes(color = id, size = node.size[id]/300), show.legend = FALSE) +
geom_edge_label(size = 6, colour = "red",
fontface = "bold",
shift = 0.64,
nudge_x = -0.01,
max_length = 10,
splitlevels = 1:4) +
geom_node_label(line_list = list(aes(label = paste0("Node ", id, ": ", splitvar)),
aes(label = paste0("N=", node.size[id], ", p",
ifelse(pvals < .001, "<.001",
paste0("=", round(pvals, 3)))),
size = 16)),
line_gpar = list(list(size = 16),
list(size = 16)),
ids = "inner", fontface = "bold", size = 16) +
geom_node_info() +
geom_node_label(aes(label = paste0("N = ", node.size),
fontface = "bold"),
ids = "terminal", nudge_y = 0.01, nudge_x = 0.01, size = 6) +
geom_node_plot(gglist = list(
geom_bar(aes(x = "", fill = species), size = 0.2, width = 0.9,
position = position_fill(), color = "black"),
theme_minimal(base_family = "arial", base_size = 24),
scale_fill_manual(values = c("gray50","gray55","gray60",
"gray70","gray80","gray85",
"blue","gray95")),
xlab(""),
ylab("Probability"),
geom_text(aes(x = "", group = species,
label = stat(count)),
stat = "count", position = position_fill(),
vjust = 1., size = 6)),
shared_axis_labels = TRUE, size = 1.2)
Stochastic-deterministic logical rules¶
Since only one mutational event human-to-human in region R1 from class A3 is reported in the right side of the tree, with high probability only non-humans hold the following rule:
rule <- (dat$autms == "A4" | (dat$autms == "A3" & dat$mut_type != "HRH"))
unique(as.character(dat[rule,]$species))
- ‘bolivian_monkey’
- ‘golden_monkey’
- ‘gelada_baboon’
- ‘silvery_gibbon’
- ‘chimpanzee’
- ‘bonobos’
- ‘gorilla’
Only humans-to-human mutations hold the following rule:
idx <- dat$autm == "A1" & dat$regions == "R3" & (dat$mut_type == "HHY" | dat$mut_type == "YHH")
dat[ idx, ]
| autms | regions | mut_type | cube | species | |
|---|---|---|---|---|---|
| <fct> | <fct> | <fct> | <fct> | <fct> | |
| 632 | A1 | R3 | YHH | ACGT | human |
| 687 | A1 | R3 | HHY | ACGT | human |
Only non-humans hold the following rule
rule <- (dat$autms == "A4" | (dat$autms == "A3" & dat$regions != "R1"))
unique(as.character(dat[rule,]$species))
- ‘bolivian_monkey’
- ‘golden_monkey’
- ‘gelada_baboon’
- ‘silvery_gibbon’
- ‘gorilla’
- ‘chimpanzee’
- ‘bonobos’
References¶
1. Sanchez R, Morgado E, Grau R. Gene algebra from a genetic code algebraic structure. J Math Biol. 2005 Oct;51(4):431-57. doi: 10.1007/s00285-005-0332-8. Epub 2005 Jul 13. PMID: 16012800. ( PDF).
2. Robersy Sanchez, Jesús Barreto (2021) Genomic Abelian Finite Groups. doi: 10.1101/2021.06.01.446543.
3. M. V José, E.R. Morgado, R. Sánchez, T. Govezensky, The 24 possible algebraic representations of the standard genetic code in six or in three dimensions, Adv. Stud. Biol. 4 (2012) 119–152.PDF.
4. R. Sanchez. Symmetric Group of the Genetic–Code Cubes. Effect of the Genetic–Code Architecture on the Evolutionary Process MATCH Commun. Math. Comput. Chem. 79 (2018) 527-560. PDF.